On Perelmand and Yau about who proved the Poincare Conjecture

This article (see the link above) tells a great story of some of the personalities of the mathematicians involved in proving the Poincare Conjecture. It's worth the time to read it all.

The Math Was Complex, the Intentions, Strikingly Simple

George Johnson writes in the New York Times:

[M]athematics has been infused with the legend of the mad genius cut off from the physical world and dwelling in a separate realm of numbers. In ancient times, there was Pythagoras, guru of a cult of geometers, and Archimedes, so distracted by an equation he was scratching in the sand that he was slain by a Roman soldier. Pascal and Newton in the 17th century, Gödel in the 20th — each reinforced the image of the mathematician as ascetic, forgoing a regular life to pursue truths too rarefied for the rest of us to understand.

Last week, a reclusive Russian topologist named Grigory Perelman seemed to be playing to type, or stereotype, when he refused to accept the highest honor in mathematics, the Fields Medal, for work pointing toward the solution of Poincaré’s conjecture, a longstanding hypothesis involving the deep structure of three-dimensional objects. He left open the possibility that he would also spurn a $1 million prize from the Clay Mathematics Institute in Cambridge, Mass.

Unlike Brando turning down an Academy Award or Sartre a Nobel Prize, Dr. Perelman didn’t appear to be making a political statement or trying to draw more attention to himself. It was not so much a medal that he was rejecting but the idea that in the search for nature’s secrets the discoverer is more important than the discovery.

“I do not think anything that I say can be of the slightest public interest,” he told a London newspaper, The Telegraph, instantly making himself more interesting. “I know that self-promotion happens a lot and if people want to do that, good luck to them, but I do not regard it as a positive thing.”

Johnson goes on to give a half-baked, half hearted attempt to describe Perelman's refusal to accept the Fields Medal for his solution to the Poincare Conjecture. Unfortunately, Johnson really misses the point. Here is a man who just wants to think about mathematics and study nature with his own intellect. It is a state of being few of us will ever reach yet we ought to be in awe of anyone who can do this.

In a society steeped in self-promotion for the slightest contribution to any field, we find a man who contributed to the Poincare-conjecture, proved it, and wants to leave that knowledge to others without interference. This is perhaps the most noble gesture we are likely to ever find.

The only person I know who comes close to this but misses by much is Richard Feynman who wanted to turn down the Nobel prize in physics because it would interfere with his work. Feynman accepted the prize, bought a second house with the money, and continued to work.

Perelman is not interested in a second house, wants to live where he is, and be left alone. Is there anything wrong with that?

Astronomy Picture of the Day

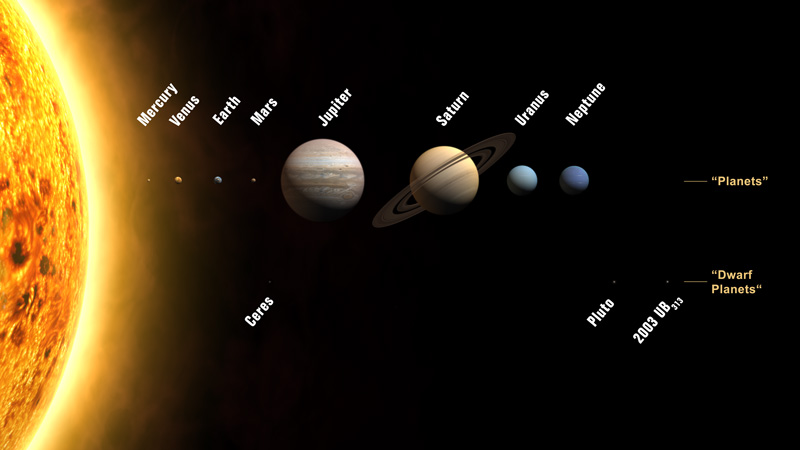
The International Astronomical Assocication demoted Pluto to a Dwarf Planet. So, our soloar system has only eight planets now.

In truth, who really cares? The idea that A is a planet and B is not a planet is semantics. A is some object in the solar system and it has a mass, location, orbit, etc. B is some other object in the solar system with its own mass, location, orbit, etc. The fact that A is more massive than B is relevant to how we calculate its effects and parameters. There are still these objects in space, regardless of how anyone classifies them.

Astronomy Picture of the Day

This cloud is from flares ejected from a C-17 plane. The pattern, that looks like an owl, results from the air flow over the wings, called wingtip vortices.

Pizza Fraud

A fraudster contacts an AT&T service rep and says he works at a pizza parlor and that the phone is having trouble. Until things get fixed, he requests that all incoming calls be forwarded to another number, which he provides.

Pizza orders are thus routed by AT&T to the fraudster's line. When a call comes in, the fraudster pretends to take the customer's order but says payment must be made in advance by credit card.

The unsuspecting customer gives his or her card number and expiration date, and before you can say "extra cheese," the fraudster is ready to go on an Internet shopping spree using someone else's money.

John Britton, an AT&T spokesman, confirmed the contents of the memo and said two separate instances of the call-forwarding scam have been reported so far in Southern California.

This came from Bruce Schneier's blog.

Poincare conjecture: Solved?

"Three years ago, a Russian mathematician by the name of Grigory Perelman, a k a Grisha, in St. Petersburg, announced that he had solved a famous and intractable mathematical problem, known as the Poincaré conjecture, about the nature of space.

After posting a few short papers on the Internet and making a whirlwind lecture tour of the United States, Dr. Perelman disappeared back into the Russian woods in the spring of 2003, leaving the world’s mathematicians to pick up the pieces and decide if he was right.

Now they say they have finished his work, and the evidence is circulating among scholars in the form of three book-length papers with about 1,000 pages of dense mathematics and prose between them.

As a result there is a growing feeling, a cautious optimism that they have finally achieved a landmark not just of mathematics, but of human thought."

Dr. Grigory Perelman has proved the Poincare conjecture. While I don't begin to understand the conjecture, at least in a fundamental sense, much less its implications, this is great news for mathematics as well as science in general.

Every step to solving one of the truly remarkable problems of our time, for example, Fermat's Last Theorem, is another step to improving human thought and human experiences.

String Theory: All theory, no substance

Time Magazine has a short article about two books that question string theory:

[D]espite its extraordinary popularity among some of the smartest people on the planet, string theory hasn't been embraced by everyone--and now, nearly 30 years after it made its initial splash, some of the doubters are becoming more vocal. Skeptical bloggers have become increasingly critical of the theory, and next month two books will be hitting the shelves to make the point in greater detail. Not Even Wrong, by Columbia University mathematician Peter Woit, and The Trouble with Physics, by Lee Smolin at the Perimeter Institute for Theoretical Physics in Waterloo, Ont., both argue that string theory (or superstring theory, as it is also known) is largely a fad propped up by practitioners who tend to be arrogantly dismissive of anyone who dare suggest that the emperor has no clothes.

So, it's a fad that has shown absolutely nothing! No predictions that can be tested anyway.

That lack of specificity hasn't slowed down the string folks. Maybe, they've argued, there really are an infinite number of universes--an idea that's currently in vogue among some astronomers as well--and some version of the theory describes each of them. That means any prediction, however outlandish, has a chance of being valid for at least one universe, and no prediction, however sensible, might be valid for all of them.

That sort of reasoning drives critics up the wall. It was bad enough, they say, when string theorists treated nonbelievers as though they were a little slow-witted. Now, it seems, at least some superstring advocates are ready to abandon the essential definition of science itself on the basis that string theory is too important to be hampered by old-fashioned notions of experimental proof.

This is called being wedded to an idea no matter what. It's bad in general and terribly awful for science.

And it is that absence of proof that is perhaps most damning. Physicists have a tolerance for theory; indeed, unless you were there to witness a phenomenon yourself--the Big Bang, say--it will always be, at some level, hypothetical. But the slow accretion of data and evidence eventually eliminates reasonable doubt. Not so--or at least not yet--with strings.

"It's fine to propose speculative ideas," says Woit, "but if they can't be tested, they're not science." To borrow the withering dismissal coined by the great physicist Wolfgang Pauli, they don't even rise to the level of being wrong. That, says Sean Carroll of the University of Chicago, who has worked on strings, is unfortunate. "I wish string theorists would take the goal of connecting to experiment more seriously," he says. "It's true that nobody has any good idea of how to test string theory, but who's to say someone won't wake up tomorrow morning and think of one? The reason so many people keep working on it is that, whatever its flaws, the theory is still more promising than any other approach we have."

In the end, scientists should accept string theory because it's the best physics has. I guess that's right up there with believing the sun revolves around the earth. It's a good theory and was at one time the best around, why should anyone have ever questioned it. And that theory had something string theory doesn't: At least you could see the sun and the earth.

It's all how you see it

I read this today on the link above and thought it worth reading for others:

A man who lived on the northern frontier of China was skilled in interpreting events. One day for no reason, his horse ran away to the nomads across the border. Everyone tried to console him, but his father said, "What makes you so sure this isn't a blessing?" Some months later his horse returned, bringing a splendid nomad stallion. Everyone congratulated him, but his father said, "What makes you so sure this isn't a disaster?" Their household was richer by a fine horse, which the son loved to ride. One day he fell and broke his hip. Everyone tried to console him, but his father said, "What makes you so sure this isn't a blessing?"
A year later the nomads came in force across the border, and every able-bodied man took his bow and went into battle. The Chinese frontiermen lost nine of every ten men. Only because the son was lame did father and son survive to take care of each other. Truly, blessing turns to disaster, and disaster to blessing: the changes have no end, nor can the mystery be fathomed.

From Chinese Fairy Tales and Fantasies, compiled by Moss Roberts, 1979, Pantheon Books

Cartoon for fun

Statistics: How they helped win World War II

This is quite amazing:

By 1941-42, the allies knew that US and even British tanks had been technically superior to German Panzer tanks in combat, but they were worried about the capabilities of the new marks IV and V. More troubling, they had really very little idea of how many tanks the enemy was capable of producing in a year. Without this information, they were unsure whether any invasion of the continent on the western front could succeed.

The statisticians had one key piece of information, which was the serial numbers on captured mark V tanks. The statisticians believed that the Germans, being Germans, had logically numbered their tanks in the order in which they were produced. And this deduction turned out to be right. It was enough to enable them to make an estimate of the total number of tanks that had been produced up to any given moment.

The basic idea was that the highest serial number among the captured tanks could be used to calculate the overall total. The German tanks were numbered as follows: 1, 2, 3 ... N, where N was the desired total number of tanks produced. Imagine that they had captured five tanks, with serial numbers 20, 31, 43, 78 and 92. They now had a sample of five, with a maximum serial number of 92. Call the sample size S and the maximum serial number M. After some experimentation with other series, the statisticians reckoned that a good estimator of the number of tanks would probably be provided by the simple equation (M-1)(S+1)/S. In the example given, this translates to (92-1)(5+1)/5, which is equal to 109.2. Therefore the estimate of tanks produced at that time would be 109

By using this formula, statisticians reportedly estimated that the Germans produced 246 tanks per month between June 1940 and September 1942. At that time, standard intelligence estimates had believed the number was far, far higher, at around 1,400. After the war, the allies captured German production records, showing that the true number of tanks produced in those three years was 245 per month, almost exactly what the statisticians had calculated, and less than one fifth of what standard intelligence had thought likely.

Emboldened, the allies attacked the western front in 1944 and overcame the Panzers on their way to Berlin. And so it was that statisticians won the war - in their own estimation, at any rate.

This is a lesson for today: Intelligence over estimated the number by a factor of 5. What does that say about the intell world now?

Preditors Prefer Dimwitted Prey

I think this is true in the human world, too.

Tricks to play on your wireless free loaders

Here's a cute solution to a common problem.

Suppose you have a wireless router that people are free loading on. You could encrypt your wireless connection, which is what I do anyway, and probably most people should do, or you can play with the surfers.

This person added software to either redirect the freeloaders to another site, kittenwar, or he did something particularly clever. He forced the images to be turned upside down on whatever sites they visited. Take a look. (Hat tip: Schneier blog.)

Book Review: Essential Mathematics and Statistics for Science

Here isa book review I wrote for the Mathematical Association of America's website:

What is a good way to learn and compute statistics? Is it to pick-up one book, read it, and apply the algorithms to one's problem? Should one have a single book for his/her work or many books? How much theory should one know? Lastly, how can one use the world-wide web with a text book?

Drs. Currell and Dowman have written a statistics textbook for students and researchers. Their book provides brief discussions, formulas, worked examples, and exercises (with short answers in the back) to illustrate topics and usage. In addition to the text itself, there is a well-organized and useful web site for the book (http://eu.wiley.com//legacy/wileychi/currellmaths/ or http://www.wileyeurope.com/go/currellmaths). The web site provides supplementary help, in-depth solutions, and study resources, among other topics. The text and web site complement one another and are excellent at giving the reader a workable grasp of the material.

The text begins with a gentle discussion of statistics, data, and numbers. It discusses units, conversion between units, and then measurements. The discussion and topics are a solid introduction for the beginning student. The book then guides the reader through manipulation of equations, relationships between variables (such as linear, quadratic and exponential) and discusses probability distributions such as normal, binomial, and Poisson. In the final chapters the book discusses statistical tests: F-test, t-test, Chi squared, and non-parametric tests. All these topics are highly relevant to researchers, well presented, and easy to follow. The multitude of examples clarifies the text.

The authors state in the first sentence that the book is for "biological, environmental, chemical, forensic, and sport sciences." This is important because the book, which presents the material at that level, is not the most appropriate for mathematicians, physicists or engineers—anyone with a deeper mathematical background or interest. I was, in fact, struck by the oftentimes cook-book nature of the discussion.

I would have liked more discussion of the mathematics behind the ideas. For example, the method of linear fit is given without any theory such as derivatives. The text shows how to find the parameters with Excel but not what the Excel routines do. Many readers probably have Excel and for those who just want the answer, that may be all they need. (One note: While Excel is popular I urge authors to look at OpenOffice software, www.openoffice.org, in the future. It is free, easy to use, and not proprietary.)

What about using the world-wide web? The authors employ the web for detailed solutions and supplementary help for the reader. This is indeed a plus. Obviously, other web sites can provide details on any topic one desires. But, I believe that having a text book with the web site is the better way to use the web. The reader sees a consistent presentation of each topic both on his paper page and his screen page. The textbook gives the researcher an easy to navigate source of topic, explanation, example, without having to load pages, or search multiple sites for details. Thus this book with its companion web site are all the better.

New addition to my family

Please help me welcome our new dog, Bailey, to the family. Bailey is a pure bred golden retriever and was born on April 7, 2006. We brought her home this past Sunday and she has taken to our family very well. She's playful, active, and sweet; everything a golden is supposed to be. Plus, she retrieves!